
Mesin Turing adalah model yang sangat sederhana dari komputer. Secara esensial, mesin Turing adalah sebuah finite automaton yang miliki sebuah tape tunggal dengan panjang tak terhingga yang dapat membaca dan menulis data. Mesin Turing menggunakan notasi seperti ID-ID pada PDA untuk menyatakan konfigurasi dari komputasinya. Stack pada PDA memiliki keterbatasan akses. Elemen yang dapat diakses hanya elemen yang ada pada top stack. Pada Mesin Turing, memori akan berupa suatu tape yang pada dasarnya merupakan array dari sel-sel penyimpanan.
Visualisasi dari sebuah mesin Turing diberikan oleh gambar berikut:
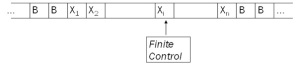
Mesin terdiri dari sebuah finite control, yang dapat berada dalam sebuah himpunan berhingga dari state. Terdapat sebuah tape yang dibagi ke dalam kotak-kotak atau sel-sel. Setiap sel dapat menampung sebuah dari sejumlah berhingga dari simbol. Pada awalnya, input yang merupakan string dari simbol dengan panjang berhingga dipilih dari input alphabet, ditempatkan pada tape. Sel-sel tape yang lain, perluasan secara infinite ke kiri dan ke kanan, pada awalnya menampung simbol khusus yang dinamakan blank. Blank bukan sebuah input symbol, dan mungkin terdapat simbol tape yang lain disamping input symbol dan blank. Terdapat sebuah tape head yang selalu ditempatkan pada salah satu dari sel-sel tape. Mesin turing dikatakan men-scan sel tersebut. Pada awalnya, tape head berada pada sel paling kiri yang menampung input. Sebuah pergerakan mesin Turing adalah sebuah fungsi dari state dari finite control dan tape symbol yang di-scan.
Dalam satu pergerakan, mesin Turing akan:
- Merubah state. Next state dapat sama dengan current state.
- Menulis sebuah tape symbol dalam sel yang di-scan. Tape symbol ini mengganti symbol apapun yang ada dalam sel tersebut. Secara opsional, simbol yang dituliskan dapat sama dengan simbol yang sekarang ada dalam tape.
- Memindahkan tape head ke kiri atau ke kanan.
Notasi formal Mesin Turing
Mesin Turing dijelaskan oleh 7-tuple:
M = (Q, S, G, d, q0, B, F)
Komponen-komponennya adalah:
- Q: Himpunan berhingga dari state dari finite control.
- S: himpunan berhingga dari simbol-simbol input.
- G: Himpunan dari tape symbol. S merupakan subset dari G.
d: Fungsi transisi. Argumen d(q, X) adalah sebuah state q dan sebuah tape symbol X. Nilai dari d(q, X), jika nilai tersebut didefinisikan, adalah triple (p, Y, D), dimana:
- p adalah next state dalam Q
- Y adalah simbol, dalam G, ditulis dalam sel yang sedang di-scan, menggantikan simbol apapun yang ada dalam sel tersebut.
- D adalah arah, berupa L atau R, berturut-turut menyatakan left atau right, dan menyatakan arah dimana head bergerak.
q0: start state, sebuah anggota dari Q, dimana pada saat awal finite control ditemukan.
B: simbol blank. Simbol ini ada dalam G tapi tidak dalam S, yaitu B bukan sebuah simbol input.
F: himpunan dari final state, subset dari Q.
Deskripsi Instantaneous (ID) untuk Mesin Turing
ID digunakan untuk mengetahui apa yang mesin Turing kerjakan. ID direpresentasikan oleh string X1X2X3… Xi-1qXiXi+1 … Xn, dimana:
– q adalah state dari TM
– Tape head men-scan simbol ke-i dari kiri.
– X1X2 …Xn adalah bagian dari tape di antara nonblank pada sel paling kiri dan paling kanan.
Pergerakan TM M = (Q, S, G, d, q0, B, F) dinyatakan oleh notasi ├ atau ├. ├*M atau ├*digunakan untuk menunjukkan nol, satu atau lebih pergerakan dari TM.
Anggap d(q, Xi) = (p, Y, L), yaitu pergerakan selanjutnya adalah ke kiri. Maka
X1X2… Xi-1qXiXi+1 … Xn
├ X1X2… Xi-2pXi-1 YXi+1 … Xn
Pergerakan ini menyatakan perubahan ke state p. Tape head sekarang diposisikan di sel i-1.
Jika i = n dan Y = B maka simbol B yang ditulis pada Xn berhubungan dengan urutan tak hingga dari blank–blank yang mengikuti dan tidak muncul dalam ID selanjutnya. Dengan demikian
X1X2 …Xn-1 q Xn├ X1X2… Xn-2p Xn-1
Terdapat dua pengecualian:
– Jika i=1, maka M bergerak ke blank ke bagian kiri dari X1. Dalam kasus ini,
qX1X2 …Xn├ pBYX2… Xn
– Jika i = n dan Y = B maka simbol B yang ditulis pada Xn berhubungan dengan urutan tak hingga dari blank–blank yang mengikuti dan tidak muncul dalam ID selanjutnya. Dengan demikian
X1X2 …Xn-1 q Xn├ X1X2… Xn-2p Xn-1
Anggap d(q, Xi) = (p, Y, R), yaitu pergerakan selanjutnya adalah ke kanan. Maka
X1X2… Xi-1qXiXi+1 … Xn ├ X1X2… Xi-1 YpXi+1 … Xn
Tape head telah bergerak ke sel i+1. Terdapat dua pengecualian:
– Jika i = n, maka sel ke-i+1 menampung sebuah blank, dan sel tersebut bukan bagian dari ID sebelumnya. Dengan demikian
X1X2 … Xn-1 qXn├ X1 X2… Xn-1YpB
– Jika i = 1 dan Y = B maka simbol B yang ditulis pada X1 berhubungan dengan urutan tak hingga dari blank–blank dan tidak muncul dalam ID selanjutnya. Dengan demikian
qX1X2 …Xn├ pX2… Xn
Diagram Transisi untuk Mesin Turing
Diagram transisi terdiri dari sebuah himpunan dari node–node yang menyatakan state–state dari Mesin Turing .sebuah arc dari state q ke state p diberi label oleh satu atau lebih item dengan bentuk X/Y D, dimana X dan Y adalah tape symbol, dan D adalah arah, kiri (L) atau kanan (R). Bahwa bila d(q, X) = (p, Y, D) diperoleh label X/Y D pada arc dari q ke p. Dalam diagram arah D dinyatakan dengan tanda ¬ untuk “left” dan ® untuk “right”. Start state ditandai dengan kata “start” dan sebuah panah yang masuk ke dalam state tersebut. Final state ditandai dengan putaran ganda.
Contoh:
Mesin Turing berikut menghitungan fungsi , yang dinamakan monus atau propersubstraction. Fungsi ini didefinisikan oleh m n = max(m – n, 0). Bahwa, m n = m – n jika m ³ n dan 0 jika m < n. Mesin Turing yang melakukan operasi ini adalah
M = ({q0, q1, … , q6}, {0, 1}, {0, 1, B}, d, q0, B)
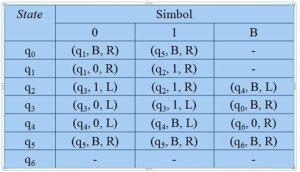
Aturan untuk fungsi transisi d:
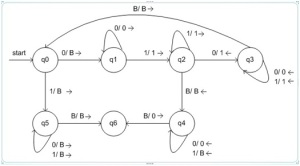
Diagram transisi dari mesin Turing M:
Daftar Pustaka
John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman. 2001. Introduction to Automata Theory, Languange, and Computation. Edisi ke-2. Addison-Wesley
Sumber :nurmnabil27.wordpress-com


.jpg)





